The control of stochastic processes refers to identifying the optimal input settings to achieve the desired output performance. This is a widely studied problem in the optimization community.

Example: Control of key performance indicators in manufacturing systems

Key Performance Indicators (KPIs), e.g., throughput and initialization, are designed to measure critical system objectives and conduct performance evaluation and control of complex manufacturing systems. In practice, we often need to control the system KPI to be at a certain level to optimize the operation and maximize the profit.

In manufacturing systems, the stochastic queueing model is often used to study the KPI modeling and control problem. See Figure 5 for a serial stochastic queueing that represents a manufacturing system.

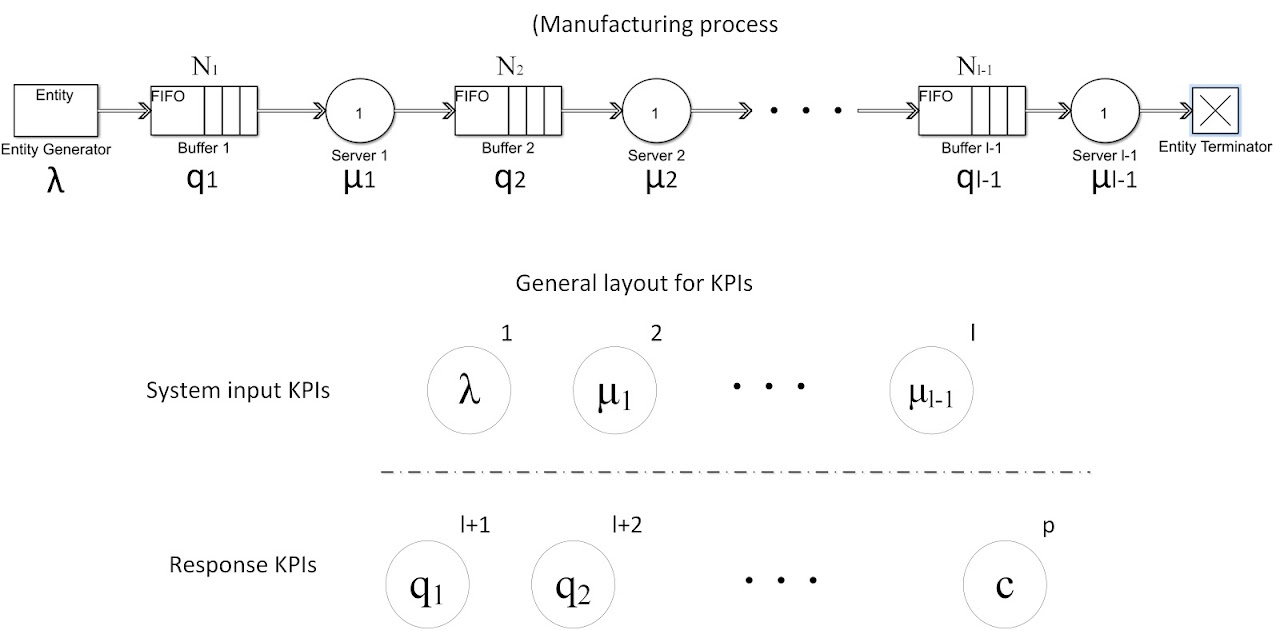
Figure 5. KPIs in a manufacturing system are represented by the queueing network.

The challenge in KPI control for manufacturing systems is that the randomness of output (response) KPIs depends on the value of the input KPIs. For example, the cycle time distribution depends on the value of the arrival rate and server rate. This makes KPI control a decision-dependent stochastic optimization, which is in general hard to solve. The key idea to deal with this challenging problem is to strategically break the dependence between the randomness of output KPIs and the input KPI values.